0
Add funds
Fund 1
Fund 2
Fund 3
Fund 4
Contact us
Contact Nuveen
Thank You
Thank you for your message. We will contact you shortly.
Municipal Bonds
Rolling down the yield curve in up and down markets
Through active management, institutional investors in municipal bonds can employ professional strategies that seek to overcome market complexities and take advantage of profitable opportunities. One such strategy, which may be difficult for individual investors to implement due to transaction costs, is called “rolling down the yield curve.”
Returns may be enhanced by selling a bond at its peak price and rolling into a longer maturity bond. Two principles make this strategy viable:
- Bonds with longer maturities typically have higher yields to compensate investors for a longer period of uncertainty.
- Bonds with lower yields have higher prices, assuming coupon rates and maturity remain the same.
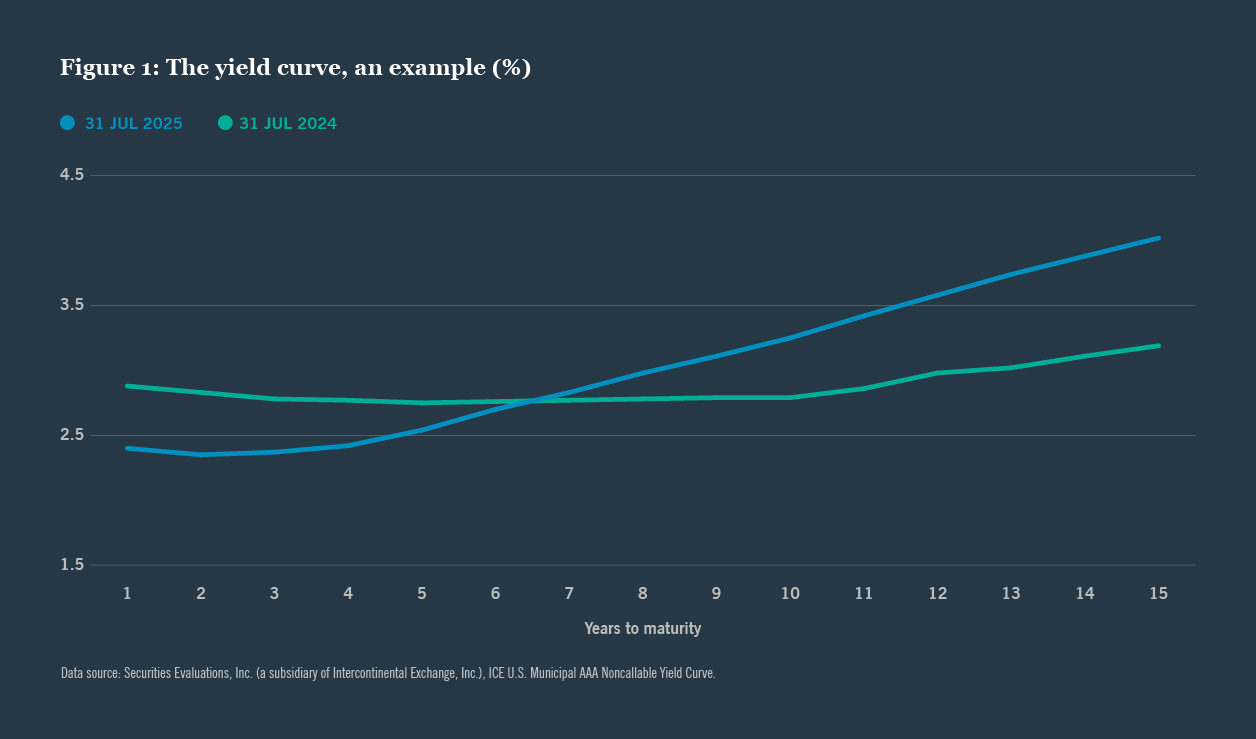
The yield curve
The first principle can be visualized by plotting a yield curve. If one charts yields on the Y-axis, and time to maturity on the X-axis, the resulting line will usually slope upward to the right. However, aggressive increases in the fed funds rate by the U.S. Federal Reserve in 2022 and 2023 have inverted the yield curve. Interest rates on bonds due in five years are lower than those for bonds due in earlier years (Figure 1). For our analysis, what matters is that the yield curve slopes upward between 5 and 15 years.
The effect of rate changes should average out if the strategy is consistently followed over time.
Related articles
State ballot initiatives can significantly alter government revenue streams, project funding and fiscal stability. These changes directly affect a municipality’s financial outlook and its ability to service debt, potentially affecting bond ratings and borrowing costs.
The Nuveen Muni Monitor is a guide that informs our discussions and debate around the unique landscape of the U.S. municipal bond market.
Airport revenue bonds play an essential role in financing the U.S. airport system. Market trends may signal prospects for essential facility upgrades – and ultimately, a better air travel experience – in the coming months and years.
These examples are hypothetical and in no way intended to represent the performance of any investment. The reader should not assume that investment in any securities or asset class listed in this report were or will be profitable. This report contains no recommendation to buy or sell any specific securities and should not be considered investment advice of any kind. Certain information was obtained from third party sources, which we believe reliable but not guaranteed.
Endnotes
The views and opinions expressed are for informational and educational purposes only as of the date of production/writing and may change without notice at any time based on numerous factors, such as market or other conditions, legal and regulatory developments, additional risks and uncertainties and may not come to pass. This material may contain “forward looking” information that is not purely historical in nature. Such information may include, among other things, projections, forecasts, estimates of market returns, and proposed or expected portfolio composition. Any changes to assumptions that may have been made in preparing this material could have a material impact on the information presented herein by way of example. Performance data shown represents past performance and does not predict or guarantee future results.. Investing involves risk; principal loss is possible.
All information has been obtained from sources believed to be reliable, but its accuracy is not guaranteed. There is no representation or warranty as to the current accuracy, reliability or completeness of, nor liability for, decisions based on such information and it should not be relied on as such. For term definitions and index descriptions, please access the glossary on nuveen.com. Please note, it is not possible to invest directly in an index.
A word on risk
Investing involves risk; principal loss is possible. Investing in municipal bonds involves risks such as interest rate risk, credit risk and market risk. The value of the portfolio will fluctuate based on the value of the underlying securities. There are special risks associated with investments in high yield bonds, hedging activities and the potential use of leverage. Portfolios that include lower rated municipal bonds, commonly referred to as “high yield” or “junk” bonds, which are considered to be speculative, the credit and investment risk is heightened for the portfolio. Bond insurance guarantees only the payment of principal and interest on the bond when due, and not the value of the bonds themselves, which will fluctuate with the bond market and the financial success of the issuer and the insurer. No representation is made as to an insurer’s ability to meet their commitments. This information should not replace an investor’s consultation with a professional advisor regarding their tax situation. Nuveen Asset Management is not a tax advisor. Investors should contact a tax professional regarding the suitability of tax-exempt investments in their portfolio. If sold prior to maturity, municipal securities are subject to gain/losses based on the level of interest rates, market conditions and the credit quality of the issuer. Income may be subject to the alternative minimum tax (AMT) and/or state and local taxes, based on the state of residence. Income from municipal bonds held by a portfolio could be declared taxable because of unfavorable changes in tax laws, adverse interpretations by the Internal Revenue Service or state tax authorities, or noncompliant conduct of a bond issuer. It is important to review your investment objectives, risk tolerance and liquidity needs before choosing an investment style or manager.
Nuveen, LLC provides investment solutions through its investment specialists.
Contact us
Financial professionals
Individual investors
You are on the site for: Financial Professionals and Individual Investors. You can switch to the site for: Institutional Investors or Global Investors
Please be advised, this content is restricted to financial professional access only.
Login or register as a financial professional to gain access to this information.
Not registered yet? Register
You are about to access our website for visitors outside of the United States.
You are about to access our website for Nuveen Global Cities REIT
You are leaving the Nuveen website.
You are leaving the Nuveen website and going to the website of the MI 529 Advisor Plan, distributed by Nuveen Securities, LLC.The Nuveen website for institutional investors is available for you.
You are about to access our website for visitors outside of the United States.
You are about to access our website for Nuveen Churchill Private Capital Income Fund (“NC - PCAP”)
